Přípravné příklady ke státní maturitě 6. Planimetrie zpět

1) Úsek, který se ve skutečnosti ujde deseti kroky, je na plánu znázorněn úsečkou délky 1 cm. Kruh na plánu má poloměr 2,5 cm.

Vypočítejte, kolika kroky se obejde po obvodu skutečný kruh.

2) Ve čtvercové síti je umístěn rovnoběžník ABCD.

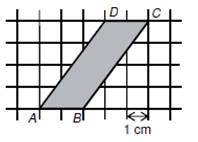
a) vypočtěte obsah rovnoběžníku ABCD a výsledek uveďte v cm².

b) V rovnoběžníku ABCD určete poměr velikostí obou výšek.

(Výsledek uveďte v základním tvaru)

3) Vzor na dlaždici tvoří čtyři shodné obdélníky a čtverec uprostřed. Obvod každého z obdélníků je 30 cm.

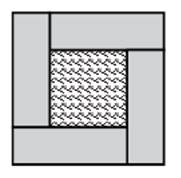
a) Vypočtěte obvod celé dlaždice (o).

b) Vypočtěte obsah dlaždice (S).

4) Do kružnice se středem S a poloměrem r = 3 cm je vepsán šedý obrazec ASBCD.

Vypočtěte v cm² obsah šedého obrazce ASBCD.

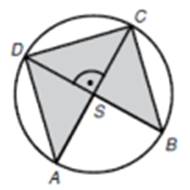
5) Délky základen lichoběžníku jsou a = 4,2 · 10⁸ metrů, c = 8 · 10⁷ metrů, výška v má velikost 4,8 · 10⁵ metrů.

Vypočtěte obsah plochy lichoběžníku.

6) Pozemek tvaru obdélníku je dočasně přerušen stavebním záborem (šedá plocha). Rovnoběžné hranice záboru na obvodu pozemku jsou dlouhé 15 m a 25 m. Jedna šikmá strana záboru, která je oplocena, má délku 236 m. Nyní se pokračuje v oplocování 190 m dlouhé strany pozemku. (Rozměry v obrázku jsou uvedeny v metrech.)

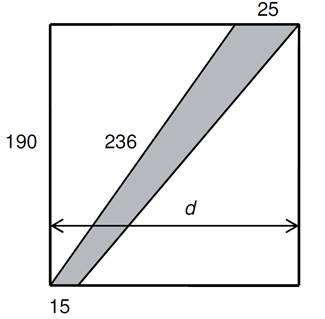
a) Vypočtěte obsah plochy stavebního záboru.

b) S přesností na celé metry vypočtěte šířku pozemku (d).

7) Okrasná část zahrady má tvar obdélníku, jehož rozměry se liší o jediný metr. Po úhlopříčce dlouhé 29 metrů vede pěšinka.

Určete délku a šířku okrasné zahrady. (Šířka pěšinky se zanedbává.)

8) Čtvercový travnatý pozemek se obchází po dvou stranáchjeho obvodu celkem třemi sty kroky. Neukázněný chodec dostal pokutu za to, že pozemek přešel po úhlopříčce.

Vypočtěte kolik kroků neukázněný chodec ušetřil a výsledek zaokrouhlete na desítky.

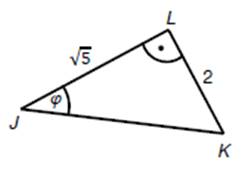
9) V trojúhelníku JKL platí: .

Určete hodnotu .

10) V pravoúhlém trojúhelníku ABC je pravý úhel při vrcholu C, úhel CAB má velikost α=60° a strana AC má délku b = .

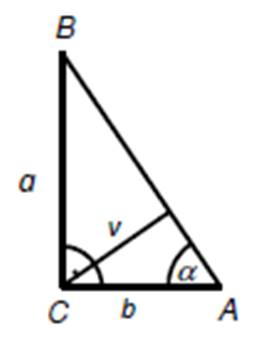
a) Vypočtěte délku strany BC.

b) Vypočtěte velikost výšky v na přeponu AB.

11) Na plánu jsou vyznačeny údaje pořízené při zaměřování vrtné věžě V za dvou stanovišť A a B.

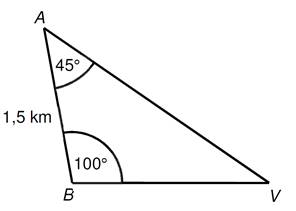
a) Určete nejmenší úhel, pod kterým je možné od věže V sledovat současně obě stanoviště A a B.

b) Určete s přesností na celé metry přímou vzdálenost stanoviště B od vrtné věže V.

12) Pozemek tvaru půlkruhu je třeba oplotit. Na rovnou část plotu se použije 28 metrů pletiva.

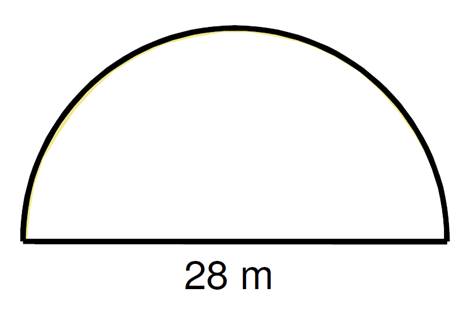
Kolik celých metrů pletuva bude nejméně potřeba na zbytek plotu po oblouku?

a) 44 metrů

b) 48 metrů

c) 52 metrů

d) 56 metrů

e) jiný počet

13) Délky stran trojúhelníku jsou 8 cm, 9 cm a 13 cm. Podobný trojúhelník má obvod o 15 cm větší.

Jaká je délka nejdelší strany podobného trojúhelníku?

a) 20 cm

b) 19,5 cm

c) 19 cm

d) 18 cm

e) jiná délka

14) Vnitřní úhel trojúhelníku ABC má velikost α = 40°. Pro délky stran platí vztah a² + b² = c².

Rozhodněte o každém z následujících tvrzení, zda je pravdivé či nikoli.

- Nejdelší strana je c.

- Největší úhel má velikost 100°.

- Trojúhelník je rovnoramenný.

- Osa strany b je rovnoběžná se stranou a.

15) Světelné paprsky svírají s vodorovnou podložkou úhel 50°. Tyč postavená kolmo k podložce je vysoká 180 cm.

Jak dlouhý stín (v cm) vrhá tyč na podložku?

16) V rovnoramenném trojúhelníku ABC se základnou AB platí: ǀACǀ = ǀBCǀ = 10; α = ǀ∡ CABǀ = 75°

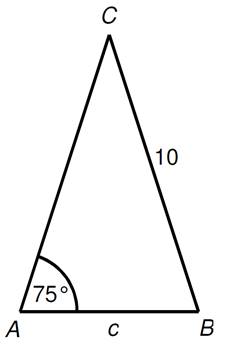
Jakou délku má základna c = ǀABǀ?

(Výsledky jsou zaokrouhleny na desetiny.)

a) 4,9

b) 5,5

c) 5,5

d) 5,8

e) jinou délku

17) Trojúhelník ABC má délky stran a = 3 cm, b = 5 cm a c = 7 cm.

Jaký je součet velikostí dvou nejmenších vnitřních úhlů trojúhelníku ABC?

a) 22°

b) 38°

c) 60°

d) 105°

e) jiný

18) Jaká je délka úhlopříčky AC vypočtená s přesností na desetiny centimetru?

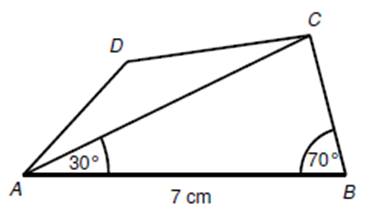
a) menší než 6,1 cm

b) 6,1 cm

c) 6,7 cm

d) 7,0 cm

e) větší než 7,0

19) Pozemek zakreslený v plánku má být rozdělen rovnou hranicí ST na dvě části.

Jaká je délka hranice ST vypočtená s přesností na desítky metrů?

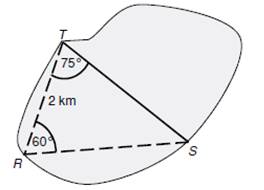
a) ǀSTǀ = 2 230 m

b) ǀSTǀ = 2 450 m

c) ǀSTǀ = 2 630 m

d) ǀSTǀ = 2 800 m

e) ǀSTǀ = 3 010 m

20) Přiřaďte ke každé úsečce její délku.

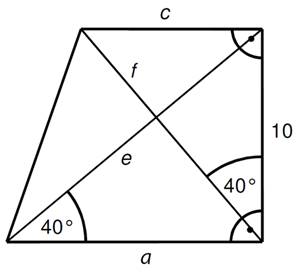- strana a

- strana c

- úhlopříčka f

21) Na obrázku jsou zakresleny tři rovinné útvary s vrcholy v mřížových bodech.

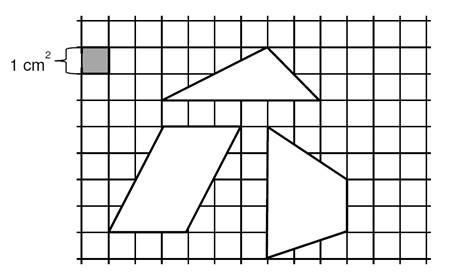
Jaký je součet obsahů všech tří rovinných obrazců?

a) menší než 27,5 cm²

b) 27,5 cm²

c) 28,0 cm²

d) 28,5 cm²

e) větší než 28,5 cm²

22) Rozvinutý plášť kužele tvoří půlkruh. Délka strany kužele je 6 cm. Jaký je obsah pláště kužele?

a) 6 cm²

b) 8 cm²

c) 9 cm²

d) 12 cm²

e) 18 cm²

23) Síť tělesa tvoří tři čtverce a dva rovnostranné trojúhelníky.

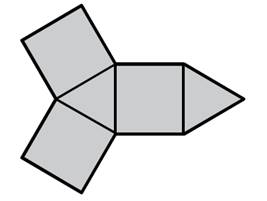Určete počet hran složeného tělesa.

24) Kolem kruhové travnaté plochy je 2 m široký chodník. Vnější okraj chodníku tvoří obrubník, jehož délka je 157 m.

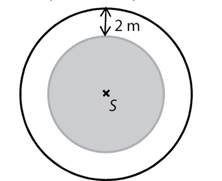
Vypočtěte obsah kruhové travnaté plochy a výsledek zaokrouhlete na desítky m². Uveďte celý postup řešení.

25) Přiřaďte ke každému trojúhelníku určenému trojicí veličin délku strany x.

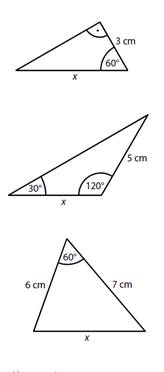
a) x < 4 cm

b) x = 4 cm

c) x = 5 cm

d) x = 6 cm

e) x > 6 cm

26) *Bod Y leží uvnitř úsečky CD. Obsah trojúhelníku ABY je roven obsahu lichoběžníku ABCD (AB ǁ CD). Vypočtěte délku strany CD lichoběžníku ABCD.

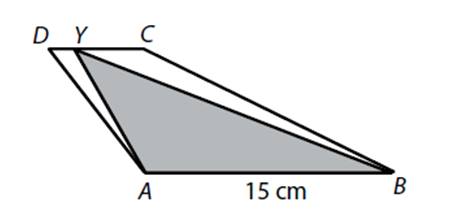
27) *Dvě části střechy domu tvoří obdélníky, které spolu svírají úhel 105°. Střecha má z každé strany jiný sklon (z levé strany 30°). V jakém poměru jsou velikosti ploch obou částí střechy?

a) 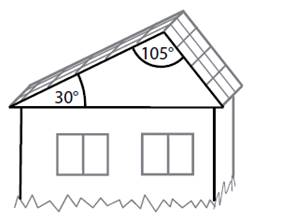3 : 2

b) 2 :

d) : 1

e) : 1

28) V rovnoramenném pravoúhlém trojúhelníku ABC s pravým úhlem při vrcholu C platí: A[-1;2], C[-5;-2]. Vypočtěte délku strany AB.

29) Ve čtyřúhelníku ABCD platí:

|AB| = 5 cm, |BC| = 5 cm, |CD| = 6 cm, |BD| = 6 cm, |∡ABD| = 90°

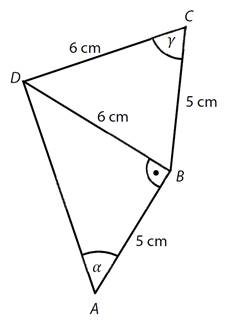
a) Určete velikost úhlu α = |∡DAB|. Výsledek zaokrouhlete na celé stupně. Uveďte celý postup řešení.

b) Určete velikost úhlu γ = |∡BCD|. Výsledek zaokrouhlete na celé stupně. Uveďte celý postup řešení.

30) Hranice LP mezi dvěma pozemky má délku 125 metrů. Od jejího levého okraje L vede rovná pěšina LM, která s touto hranicí svírá úhel o velikosti 60°.

Na pěšině je stanoviště A, z něhož je hranice LP vidět pod zorným úhlem 20°.

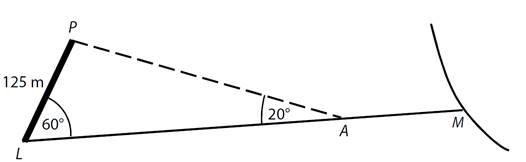
Jaká je vzdálenost AL stanovištěA od levého okraje L hranice LP? Výsledek je zaokrouhlen na celé metry.

a) 250 m

b) 343 m

c) 360 m

d) 365 m

e) jiná vzdálenost

31) Z pravoúhlého trojúhelníku ABC byl odstřižen bílý trojúhelník CED.

Platí: |AE| = 4 cm, |CE| = 2 cm, |BD| = 5 cm, |CD| = 3 cm.

Jaký je obsah tmavého čtyřúhelníku ABDE?

a) 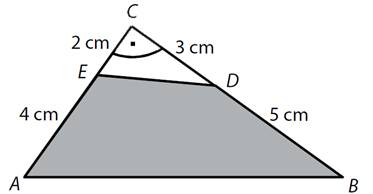21 cm²

b) 22 cm²

c) 23 cm²

d) 24 cm²

e) jiný obsah

32) Na obrázku je síť kvádru se čtvercovou podstavou.

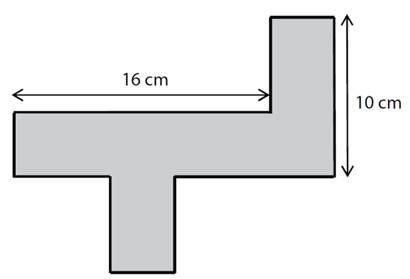Jaký je povrch kvádru?

a) 64 cm2

b) 96 cm2

c) 128 cm2

d) 144 cm2

e) jiný povrch

33) Obrazec se skládá z tmavé a bílé plochy. Tmavou plochu tvoří část čtverce ABCD a půlkruh s průměrem AD. Bílou plochu tvoří kruh se středem B a průměrem XY.

Platí: |AB| = 40 cm, |XY| = 20 cm.

Rozhodněte o každém z následujících tvrzení, zda je pravdivé, či nikoli.

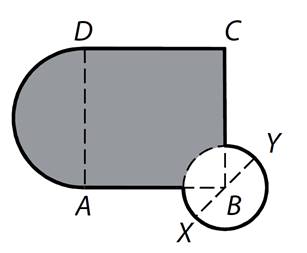- obsah tmavého půkruhu je 400π cm²

- obsah bílého kruhu je polovinou obsahu tmavého půlkruhu

- obsah bílé části čtverce ABCD je 25π cm²

- obsah bílého kruhu je 200π cm²

34) Svisle rostoucí strom je vysoký 39 m. Místo pozorování P je od paty kmene stromu vzdáleno 101 m a od vrcholu stromu 128 m. Z místa pozorování P se strom od paty kmene po vrchol jeví v zorném úhlu φ.

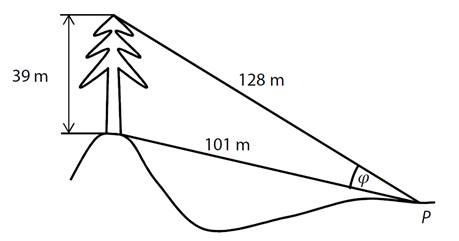
Jaké je velikost zorného úhlu φ?

(Výsledek je zaokrouhlen na celé stupně.)

a) 14°

b) 18°

c) 21°

d) 23°

e) 38°

35) V rovině jsou dány body A[0; ] a B[; ]. Jaký obvod má čtverec ABCD?

b) 22

d) 28

e) obvod nelze jednoznačně určit

36) Šestiúhelník ABCDEF je složen z bílého lichoběžníku a dvou tmavých rovnoramenných pravoúhlých trojúhelníků. Výška lichoběžníku je 4 cm, jedna jeho základna měří 6 cm a obsah lichoběžníku je 32 cm². Jaký je obsah šestiúhelníku ABCDEF?

a) 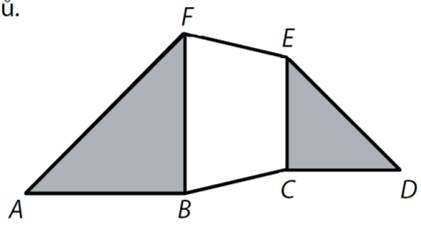74,5 cm²

b) 82 cm²

c) 90,5 cm²

d) 96 cm²

e) 100 cm²

37) V každé zobrazené situaci je šířka řeky označena symbolem s a vzdálenost AB je 50 m. Přiřaďte ke každé situaci odpovídající šířku s řeky. Výsledky jsou zaokrouhleny na celé metry.

a) 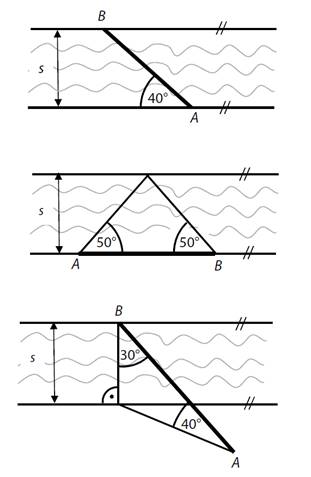méně než 28 m

b) 30 m

c) 32 m

d) 34 m

e) více než 36 m

38) Ve větru se zlomil 36 m vysoký strom. Vrchol zlomeného stromu se dotýká země, a to ve vzdálenosti 12 m od paty kmene stromu. (Tloušťku kmene zanedbáváme.) Vypočítejte, v jaké výšce nad zemí (h) se strom zlomil. Uveďte celý postup řešení.

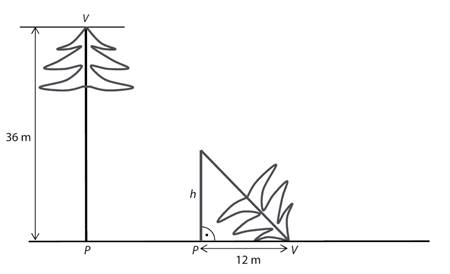
39) Na břehu řeky se žáci učili obsluhovat měřící přístroje – teodolit a laserový dálkoměr. Změřili následující údaje:

|BD| = 40 m, |∢ADB| = 20°, |∢CBD| = 50°, |∢ACD| = |∢BCD| = 90°

Jaká je šířka řeky s = |AB|?

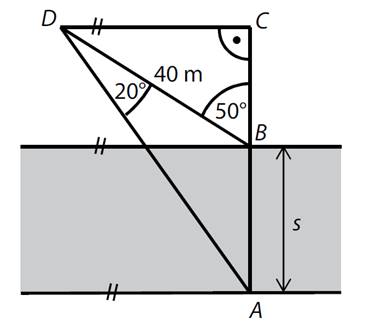
40) *Do kružnice se středem S a poloměrem 10 cm je vepsán tmavý osově souměrný obrazec. Pro velikost jeho vnitřního úhlu při vrcholu V platí: cosα = 0,6. Jaký je obsah tmavého obrazce?

a) 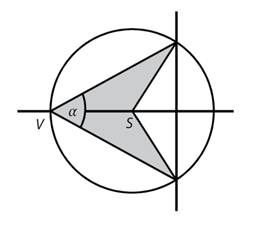menší než 60 cm²

b) 60 cm²

c) 75 cm²

d) 80 cm²

e) větší než 80 cm²

41) V trojúhelníku ABC vypočtěte bez zaokrouhlování:

a) 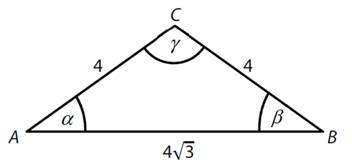velikost vnitřního úhlu γ

b) výšku v_c na stranu AB v centimetrech

(uvedené rozměry jsou uvedené v centimetrech, uveďte celý postup řešení obou částí úlohy)

42) Z místa pozorování M je možné zaměřit body K, L na obou krajích silnice v zorném úhlu φ. Platí: |ML| = 55 m, |KL| = 6 m, |∢QKM| = 55°, |∢KML| = φ, body Q, K a L leží na jedné přímce. Jaká je velikost zorného úhlu φ? (výsledek je zaokrouhlen na desetiny stupně)

a) 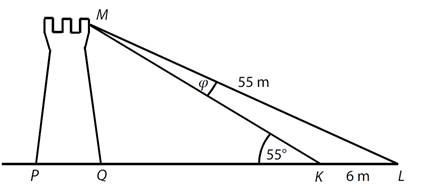5,1°

b) 6,3°

c) 7,4°

d) 8,2°

e) jiná velikost

43) V lichoběžníku ABCD o obsahu 32 cm² je výška v = 4 cm a délka jedné základny 6 cm. Lichoběžník je úhlopříčkou BD rozdělen na dva trojúhelníky ABD a BCD.

O kolik cm² se liší obsahy trojúhelníků ABD a BCD?

a) 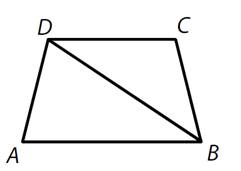o 5 cm²

b) o 6,5 cm²

c) o 7 cm²

d) o 7,5 cm²

e) o 8 cm²

44) V obdélníku ABCD o obsahu 28 cm² je umístěn trojúhelník CDE. Oba obrazce mají společnou stranu CD.

Platí: |BC| = 4 cm, |CE| = 5 cm, |DE| = 3 cm.

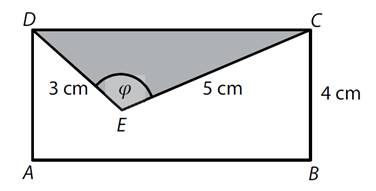
Vypočtěte velikost úhlu φ. (Uveďte postup řešení.)

45) Pětiúhelník ABCED je složen ze čtverce ABCD o obsahu 100 cm² a trojúhelníku CED o obsahu 30 cm².

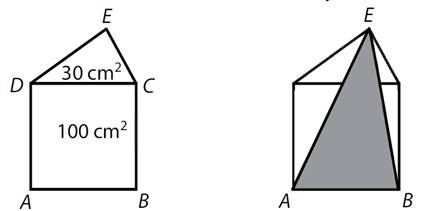
Jaký je obsah trojúhelníku ABE?

a) menší než 75 cm²

b) 75 cm²

c) 78 cm²

d) 80 cm²

e) větší než 80 cm²

Výsledky:

1)		157 kroků
2)	a)	8 cm²
	b)	5 : 2
3)	a)	o = 60 cm
	b)	S = 225 cm²
4)		13,5 cm²
5)		1,2 · 10¹⁴ m²
6)	a)	S = 3 800 m²
	b)	d = 165 m
7)		20 m x 21 m
8)		přibližně 90 kroků
9)
10)	a)	\|BC\| = a = 18
	b)	v = 9
11)	a)	35°
	b)	1 849 m
12)		a
13)		b
14)		ano, ne, ne, ano
15)		e
16)		b
17)		c
18)		c
19)		b
20)		e, d, c
21)		d
22)		e
23)		9 hran
24)		S = 1 660 m²
25)		d, c, e
26)		ǀCDǀ = 3 cm
27)		e
28)		8
29)	a)	α = 50°
	b)	γ = 65°
30)		c
31)		a
32)		c
33)		ne, ano, ano, ne
34)		a
35)		c
36)		e
37)		- c - b - d
38)		h = 16 m
39)		b
40)		d
41)	a)	γ = 120°
	b)	v_c = 2 cm
42)		a
43)		e
44)		φ = 120°
45)		d

zpět nahoru