Přípravné příklady ke státní maturitě 7. Stereometrie zpět
1) Drátěný model pravidelného šestibokého hranolu s podstavnou hranou délky a = 8 cm má výšku v = 12 cm. Těleso se přelepí papírem, podstavy tmavým a plášť bílým.

a)
Vypočtěte v cm největší možnou přímou vzdálenost dvou vrcholů
drátěného hranolu. (Tloušťku drátu
zanedbáváme.)
b)
Vypočtěte v cm2 obsah bílého papírového pláště hranolu.
2) Vypočtěte, kolik
centimetrů měří poloměr koule, jejíž objem je 1 litr. (Údaj zaokrouhlete na desetiny centimetru.)
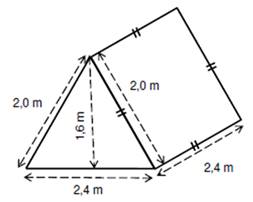
3) Vypočtěte v litrech
objem vzduchu ve stanu.
4) Nádobu tvaru pravidelného šestibokého hranolu s podstavou o obsahu 0,5 dm2 naplní tři čtvrtlitrové hrnky vody až po okraj.
Jaká
je výška nádoby?
a) 37,5 cm
b) 17 cm
c) 15 cm
d) 11,5 cm
e) Jiný výsledek
5) Koule má poloměr 0,3 m. Kolikrát větší je objem koule s dvojnásobným poloměrem?
a) devětkrát
b) osmkrát
c) šestkrát
d) třikrát
e) méně než třikrát
6) V uzavřeném skleněném kvádru s hranami délek 30 cm, 60 cm a 80 cm je obarvená kapalina. Postavíme-li kvádr na stěnu s rozměry 30 cm x 60 cm, dosáhne kapalina do výšky 40 cm. V jaké výšce bude hladina kapaliny, postavíme-li kvádr na stěnu s rozměry 30 cm x 80 cm? (Tloušťku stěn zanedbáváme.)
a) 20 cm
b) 25 cm
c) 30 cm
d) 35 cm
e) v jiné výšce
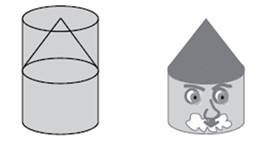
7) Z rotačního válce se vyrábí herní figura. Polovina válce je opracována na rotační kužel, který tvoří klobouk postavy.
a)
Jakou část
objemu neopracovaného válce tvoří vyrobená figura?
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
b) Obvod podstavy válce je 30 cm a strana klobouku má délku 12 cm. Jaký je povrch klobouku?
a) 1,2 dm2
b) 1,4 dm2
c) 1,5 dm2
d) 1,8 dm2
e) jiný povrch
8) Váleček se kutálí po podlaze. Po jedné celé otáčce se posune o 25 cm. Jaký je poloměr podstavy válečku? (Výsledek je zaokrouhlen na desetiny centimetru.)
a) 4,0 cm
b) 4,1 cm
c) 4,2 cm
d) 4,3 cm
e) jiný poloměr
9)
Přiřaďte ke
každé úloze její řešení (A – F)
-
Kolik stěn má krychle?
-
Kolik hran má osmiboký jehlan?
-
Kolik vrcholů má dvanáctiboký hranol?
-
Kolik stěn včetně podstav má hranol, který má 24 hran?
a)
6
b)
10
c)
12
d)
20
e)
24
f)
jiný výsledek
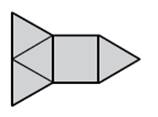
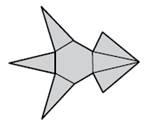
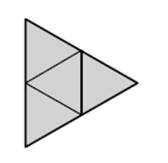
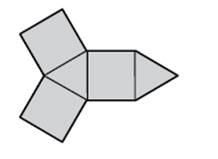
10)
Přiřaďte ke každé zakreslené
siti tělesa odpovídající název tělesa
|
10.1 |
|
10.2 |
|
|
10.3 |
|
10.4 |
|
a)
pravidelný trojboký jehlan
b)
pravidelný čtyřboký jehlan
c)
pravidelný šestiboký jehlan
d)
pravidelný trojboký hranol
e)
pravidelný šestiboký hranol
f)
nelze, útvar není sítí žádného tělesa
11)
Ve čtvercové síti je zobrazena síť kvádru. Jednotkou délky
je 1 díl, jednotkou obsahu je 1 čtverec a jednotkou objemu je 1 krychlička.
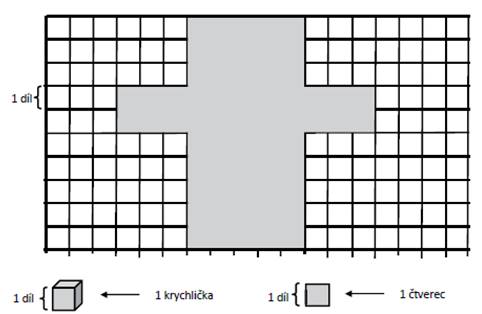
Rozhodněte o každém z následujících tvrzení, zda je
pravdivé (ANO), či nikoli (NE).
-
Nejmenší stěna kvádru má obsah 10 čtverců.
-
Největší stěna kvádru má 15 čtverců.
-
Objem kvádru je 30 krychliček.
-
Ve složeném kvádru jsou čtyři hrany s délkou 3 díly.
12)
Obytná část domu má tvar krychle a půda tvar jehlanu.
Délka hrany krychle je 16 m a výška jehlanu 6 m.
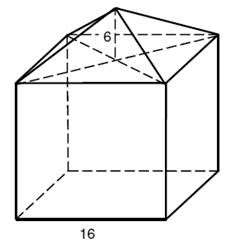
Uvedené rozměry jsou v metrech.
Jak veliká je plocha střechy?
a)
192 m2
b)
202 m2
c)
320 m2
d)
448 m2
e)
512 m2
13) Káď tvaru kvádru je vodou naplněna po okraj. Vnější rozměry kádě jsou 95 cm, 120 cm a 60 cm. Tloušťka všech stěn i dna je 5 cm.
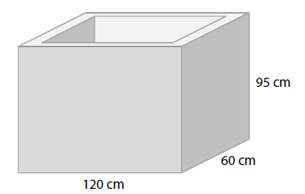
Kolik litrů vody se vešlo do kádě?
a) méně než 57 litrů
b) 467,5 litrů
c) 495 litrů
d) 4 675 litrů
e) 56 925 litrů
14)
Rozvinutý plášť kužele tvoří půlkruh. Délka strany kužele
je 6 cm.
Jaký je obsah pláště kužele?
a)
6π cm2
b)
8π cm2
c)
9π cm2
d)
12π cm2
e)
18π cm2
15)
Síť tělesa tvoří tři čtverce a dva rovnostranné
trojúhelníky.
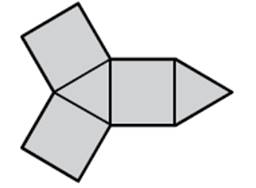
Určete počet hran složeného tělesa.
16)
Do krabice tvaru krychle je vložen válec o objemu 570 cm3.
Válec se dotýká všech stěn krabice.
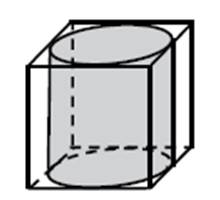
Jaká je výška válce (zaokrouhlená na desetiny cm)?
a)
menší než 8,4 cm
b)
8,5 cm
c)
8,7 cm
d)
9,0 cm
e)
větší než 9,1 cm
17)
Papírová čepice má tvar rotačního kužele. Po straně je
slepena lepící páskou. (Okraje papíru jsou k sobě přiloženy a v místě
lepení se nepřekrývají.)
Osovým řezem kužele je rovnostranný trojúhelník s délkou
strany 16 cm.

Kolik cm2 papíru je použito na čepici?
a)
96π cm2
b)
128π cm2
c)
192π cm2
d)
256π cm2
e)
jiný počet
18)
Kapka rtuti tvaru koule o průměru 3 mm se rozdělila
na dvě stejně velké kapičky tvaru koule.
Jaký je poloměr nově vytvořené kapičky rtuti? Výsledek je zaokrouhlen na
setiny mm.
a)
0,75 mm
b)
1,04 mm
c)
1,19 mm
d)
1,25 mm
e)
1,44 mm
19)
Z kvádru ABCDEFGH se vyřízne jehlan ABCDV.
Vrchol V je středem stěny EFGH.
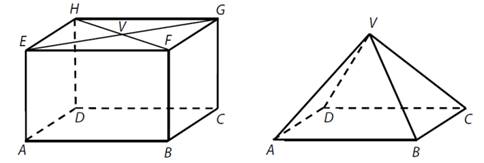
a)
Určete, kolikrát je objem
kvádru větší než objem jehlanu.
b)
Platí: |BD| = ![]() cm, |BV|
= 8 cm. Vypočítejte v cm výšku v jehlanu.
cm, |BV|
= 8 cm. Vypočítejte v cm výšku v jehlanu.
20)
Rotační válec má průměr
podstavy 12 cm a obsah pláště 60π cm2. Jaký je objem válce?
a)
36π cm3
b)
84π cm3
c)
180π cm3
d)
240π cm3
e)
jiný objem
21)
Na obrázku je síť kvádru se čtvercovou podstavou.
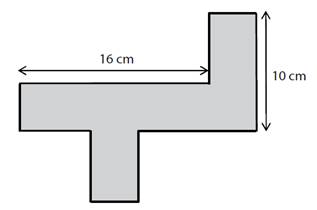
Jaký je povrch kvádru?
a)
64 cm2
b)
96 cm2
c)
128 cm2
d)
144 cm2
e)
jiný povrch
22)
Podél travnatého hřiště je natažena zahradní hadice.
V libovolné části hadice řez vedený kolmo k ose hadice vytvoří
mezikruží s vnitřním průměrem d
= 26,3 mm. (Deformaci hadice neuvažujeme.)
Jaké největší možné množství vody může obsahovat natažená
hadice délky 50m?
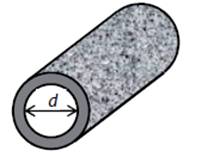 Výsledek v litrech je
zaokrouhlen na celé číslo.
Výsledek v litrech je
zaokrouhlen na celé číslo.
a)
11 litrů
b)
27 litrů
c)
86 litrů
d)
272 litrů
e)
Jiné množství vody
23)
V rovnostranném válci je vytvořena dutina tvaru
polokoule.
Poloměr podstavy válce i poloměr polokoule je r = 10 cm, výška válce je 2r.
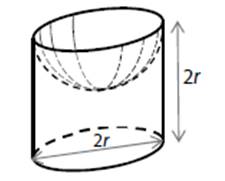
Jaký je povrch vytvořeného
tělesa (tj. válce s dutinou)?
a)
větší než 900π cm2
b)
900π cm2
c)
800π cm2
d)
700π cm2
e)
menší než 700π cm2
24)
Cvičební pomůcka z šedé tvrzené pěny je rotační
těleso, které lze popsat jako dutý válec.
Dutý válec má výšku 70 cm, vnější průměr 180 cm a vnitřní
průměr (tj. průměr dutiny) 120 cm.
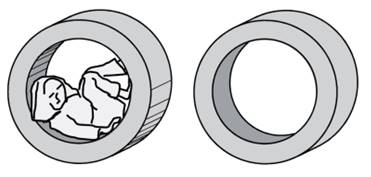
Jaký je povrch tělesa (včetně plochy uvnitř
dutiny)?
Výsledek je zaokrouhlen na desetiny m2.
a)
4,1 m2
b)
6,8 m2
c)
7,2 m2
d)
9,4 m2
e)
11,6 m2
25)
Z papírového obdélníku s rozměry 27 cm x 10 cm
se zhotoví kvádr.
Vyznačené tmavé čtverce se použijí na podstavu kvádru, bílá
část se beze zbytku rozstříhá na boční stěny kvádru.
Kvádr se po hranách spojí lepicí páskou, papír se nebude
nikde překrývat.
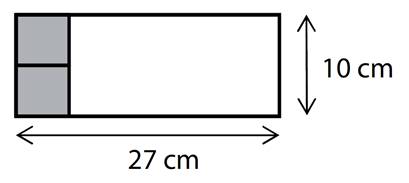
Jaký je objem kvádru?
a)
250 cm3
b)
270 cm3
c)
275 cm3
d)
550 cm3
e)
jiný objem
26)
Voda o objemu 40,5π cm3
vyplňuje ve sklenici prostor tvaru rotačního kužele.
Voda nesahá až po okraj sklenice, ale pouze do výšky 6 cm od
vrcholu kužele.
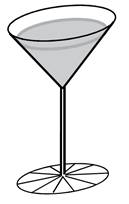
Jaký je obsah plochy sklenice smáčené vodou?
Výsledek je zaokrouhlen na desetiny cm2.
a)
51,9 cm2
b)
54,3 cm2
c)
106,0 cm2
d)
169,5 cm2
e)
211,9 cm2
Řešení
|
1) |
a) |
20 cm |
|
|
b) |
S = 576 cm2 |
|
2) |
|
r = 6,2 cm |
|
3) |
|
4 608 litrů |
|
4) |
|
c |
|
5) |
|
b |
|
6) |
|
c |
|
7) |
a) |
d |
|
|
b) |
d |
|
8) |
|
a |
|
9) |
|
a, f, e, b |
|
10) |
|
10.1 b, 10.2 c, 10.3 a, 10.4 d |
|
11) |
|
ne, ano, ano, ano |
|
12) |
|
c |
|
13) |
|
c |
|
14) |
|
e |
|
15) |
|
9 hran |
|
16) |
|
d |
|
17) |
|
b |
|
18) |
|
c |
|
19) |
a) |
3 krát |
|
|
b) |
v = 6 cm |
|
20) |
|
c |
|
21) |
|
c |
|
22) |
|
b |
|
23) |
|
d |
|
24) |
|
d |
|
25) |
|
c |
|
26) |
|
c |