Přípravné příklady ke státní maturitě 8. Analytická
geometrie zpět
1)
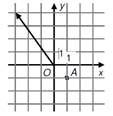
V rovině je umístěn vektor 
.
a)
Určete velikost vektoru 
.
b)
Doplňte
souřadnice libovolného vektoru
, který je k vektoru kolmý a
dvojnásobnou velikost.
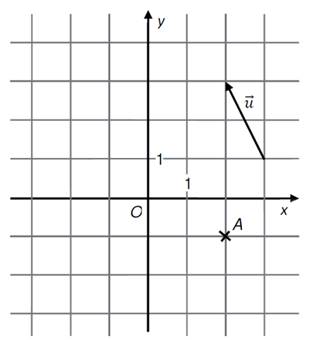
2)
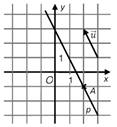
V rovině je umístěn bod A. Dále platí 
.
a)
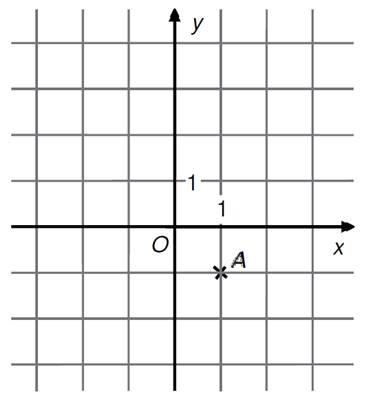Zakreslete vektor 
.
b)
Popište souřadnicemi koncový bod 
orientované úsečky 
3)
Body 
a 
jsou sousedními
vrcholy čtverce ABCD. Vypočtěte obsah čtverce ABCD.
4)
Přímka
p je určena bodem A a směrovým vektorem 
.
a) V kartézské
soustavě souřadnic Oxy sestrojte přímku p.
b) Napište
souřadnice průsečíku 
přímky p se souřadnicovou osou y.
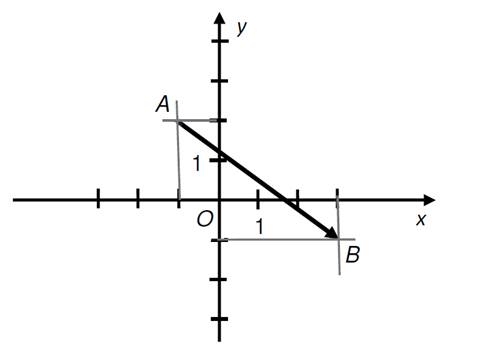
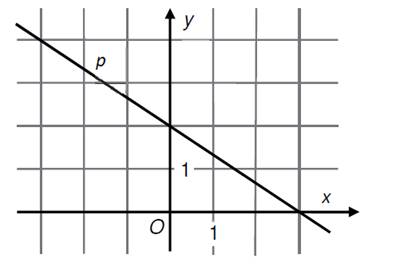
5)
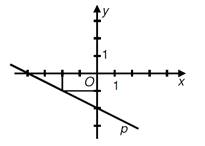
Určete rovnici
přímky p (směrnicový nebo obecný tvar) umístěné v kartézské
soustavě souřadnic Oxy.
6)
Přímka p je určena bodem 
a normálovým
vektorem 
.
a)
Zapište obecnou rovnici přímky p.
b)
V kartézskésoustavě souřadnic Oxy narýsujte přímku p.
7)
Orientovaná úsečka s počátečním bodem 
je umístěním
vektoru 
.
Který z uvedených
bodů je koncovým bodem této orientované úsečky?
a)
b)
c)
d)
e)
8)
Přímka
p procházející bodem 
má směrový vektor 
.
Která rovnice určuje
přímku p?
a)
x
– y – 2 = 0
b)
y
– 2 = 0
c)
2x
– y = 0
d)
x
+ y – 2 = 0
e)
x
– y + 2 = 0
9)
V kartézské soustavě souřadnic Oxy je
umístěna přímka p.
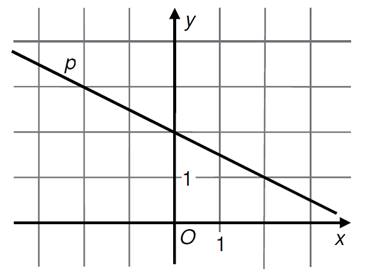
Která rovnice
určuje přímku p?
a)
2x – y + 2 = 0
b)
x – 2y + 4 = 0
c)
x – 4y – 2 = 0
d)
x + 2y – 4 = 0
e)
2x + y – 2 = 0
10)
V kartézské soustavě souřadnice Oxy je
setrojena přímka p.
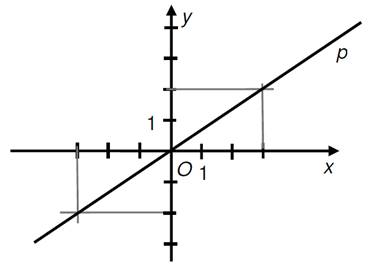
Která
z uvedených přímek a, b, c, d, e je kolmá k přímce p?
a) a: 2x – 3y + 7 = 0
b) b: 2x + 3y – 7 = 0
c) c: 2x – 3y – 7 = 0
d) d: 3x – 2y – 7 = 0
e) e: 3x + 2y + 7 = 0
11)
Trojúhelník ABC ma vrcholy 
.
Na které přímce leží
výška vc trojúhelníku ABC?
a)
p:
x – y + 2 = 0
b)
p:
3x – y – 2 = 0
c)
p:
3x + y – 10 = 0
d)
p:
x + y – 6 = 0
e)
p:
2x – y = 0
12)
V kartézské soustavě souřadnic Oxy jsou umístěny vrcholy A, B, D rovnoběžníku ABCD.
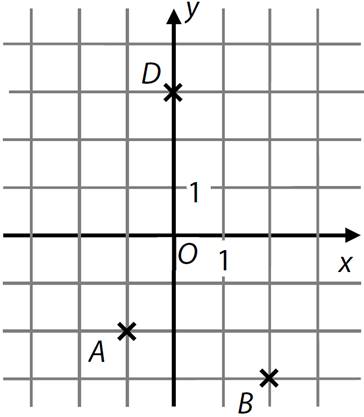
Který zápis představuje obecnou rovnici přímky AC?
a)
x + y + 3 = 0
b)
x – y – 1 = 0
c)
x – 2y – 3 = 0
d)
2x – y = 0
e)
žádný z uvedených
13)
V obdélníku ABCD jsou dány vrcholy 
a 
. Vrchol B leží na souřadnicové ose x.
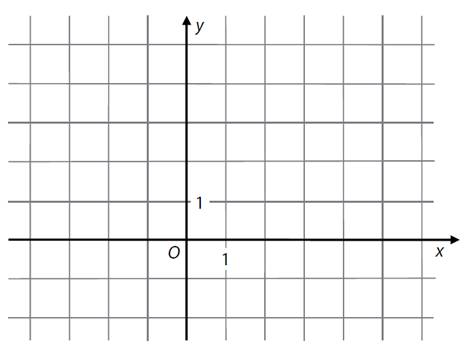
a)
Určete souřadnice směrového
vektoru přímky AB.
b)
Určete souřadnice vrcholu B.
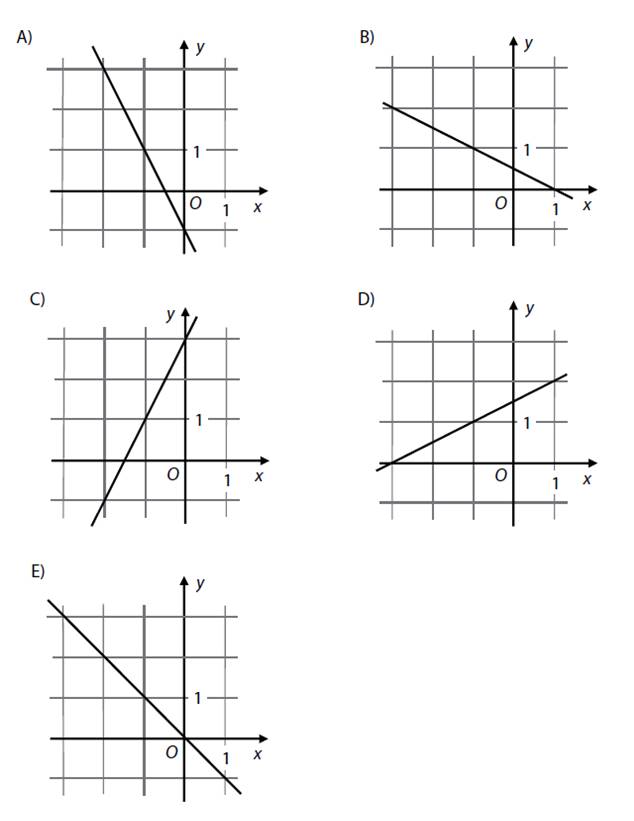
14)
Je dána přímka:
p: x = – 1 + t
y = 1 + 2t; t 
R
Na kterém obrázku je
přímka p?
15)
Je dán vektor 
a body 
.
a)
Vypočtěte chybějící souřadnici a bodu A.
b)
Vypočtěte chybějící souřadnici b bodu B.
16)
V rovnoramenném
pravoúhlém trojúhelníku ABC s pravým úhlem při vrcholu C
platí:
Vypočtěte délku strany AB.
17)
Je
dána přímka p: -12x + 4y – 5 = 0
Která
z následujících přímek je rovnoběžná s přímkou p?
a)
a:
x = 4 + 3t
y = 12 – t, 
b)
b:
x = 5 + 3t
y
= 5 + t,
c)
c:
x = 1 – t
y = 1 + 3t,
d)
d:
x = 7 + t
y = 7 + 3t,
e)
e: x = -12 – 5t
y = 4 – 5t,
18)
V kartézské
soustavě Oxy je zobrazena přímka p.
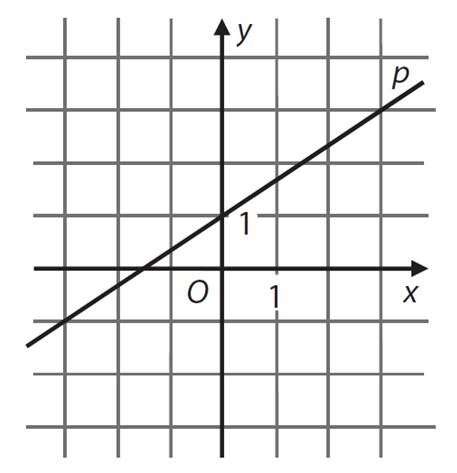
Doplňte chybějící souřadnici bodu 
a souřadnice směrového
vektoru 
přímky p.
19)
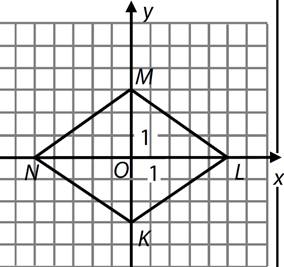
Úhlopříčky
kosočtverce KLMN leží na souřadnicových osách.
Platí: 
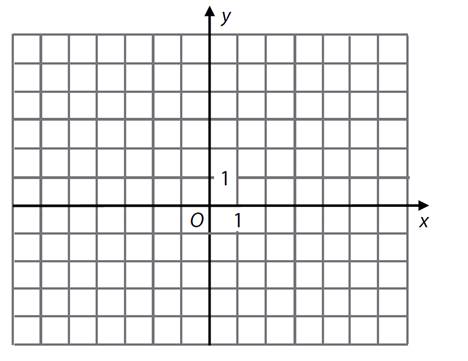
a)
V soustavě souřadnic Oxy
sestrojte kosočtverec KLMN.
b)
Vypočtěte obsah kosočtverce.
c)
Zapište obecnou rovnici přímky KL.
20)
V rovině
jsou umístěny vektory 
a 
.
K, L, M, N jsou mřížové
body.
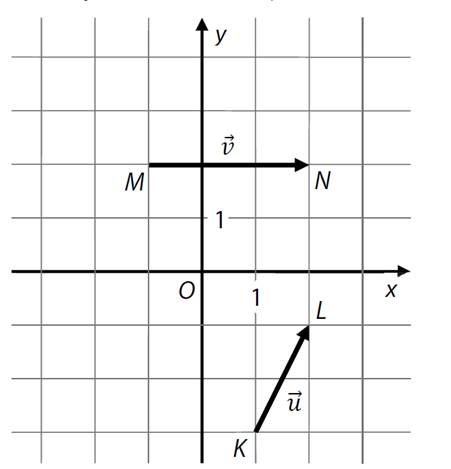
Ke každému vektoru
doplňte souřadnice (a-e) tak, aby byla splněna uvedená podmínka.
-
vektor
, kde 
-
vektor
, kde 
-
vektor
, kde 
a)
(4; 2)
b)
(2; 4)
c)
(2; -4)
d)
(-2; -4)
e)
(-4; 2)
21)
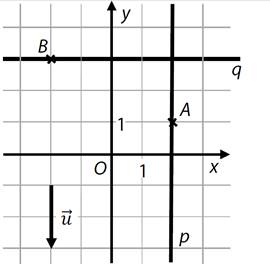
Přímka p je
určena bodem A a směrovým vektorem 
.
Přímka q prochází bodem B a je kolmá k přímce p.
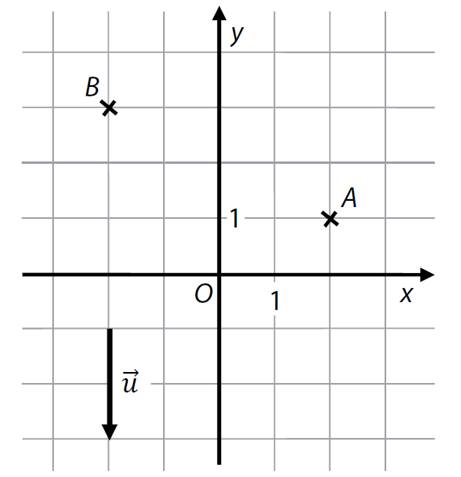
(Body A, B i počáteční a koncový bod orientované úsečky, která je
umístěním vektoru , jsou mřížové body.)
a)
Sestrojte přímky p a q.
b)
Zapište obecnou rovnici přímky q.
22)
Je dán bod 
.
O každé
z následujících přímek a, b, c, d rozhodněte, zdali daným bodem P
prochází, či nikoli.
-
a: 
-
b: 
-
c: 
-
d: 
23)
V rovině jsou dány body 
a 
.
Jaký obvod má
čtverec ABCD?
a)
b)
c)
d)
e)
Obvod nelze jednoznačně určit.
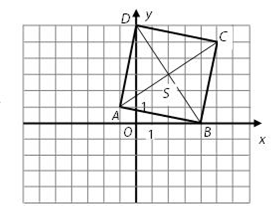
24)
Ve čtverci ABCD platí: 
a)
V kartézské soustavě souřadnic Oxy sestrojte čtverec ABCD.
b)
Zapište souřadnice středu S čtverce
ABCD.
c)
Vypočtěte velikost vektoru a výsledek uveďte
bez zaokrouhlení.
25)
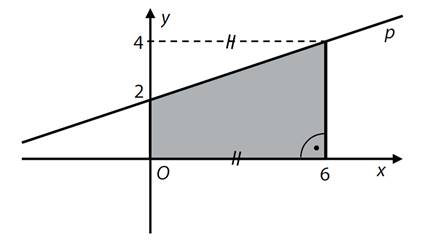
a)
Zapište obecnou rovnici přímky p.
b)
Vypočtěte odchylku přímky p a
souřadnicové osy x.
(Výsledek uveďte ve stupních a minutách.)
c)
Vypočtěte obsah tmavého obrazce.
26)
Počáteční a koncové body vektorů 
jsou umístěny
v mřížových bodech.
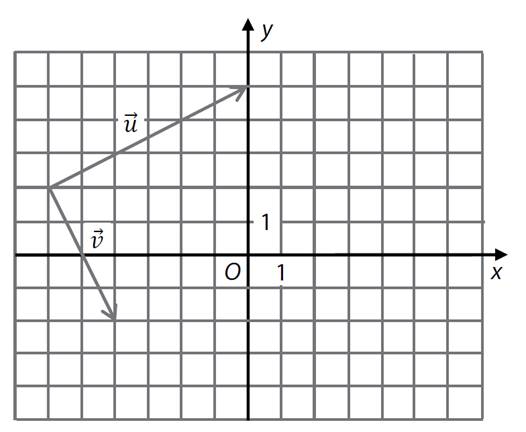
Určete
souřadnice vektoru 
.
27)
Je dána přímka p.
p: x = –4 + 2t
y = 1 – t 
Doplňte
souřadnice bodů 
, které leží na přímce p.
28)
Přímka p prochází bodem B a je kolmá
k úsečce AB.
Platí: 
.
Kterou
rovnicí je určena přímka p?
a)
5x – 2y – 8 = 0
b)
5x + 2y – 12 = 0
c)
2x – 5y + 1 = 0
d)
2x + 5y – 9 = 0
e)
žádnou z výše uvedených
29)
Umístěním vektoru je orientovaná
úsečka, jejíž počáteční i koncový bod leží v mřížovém bodě.
Vektor 
je k vektoru kolmý.
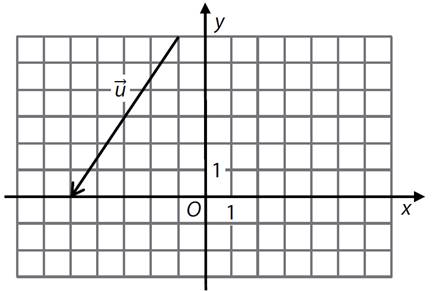
Jaká je souřadnice x vektoru ?
a)
-15
b)
-12
c)
-9
d)
-8
e)
Vektor 
nemůže být nikdy
kolmý k vektoru .
30)
Jsou dány vrcholy obdélníku ABCD:
.
Obdélníku ABCD
je opsána kružnice k.
Jaký je obsah kruhu ohraničeného kružnicí k?
a)
b)
c)
d)
e)
Výsledky:
|
1) |
a) |
|
|
|
b) |
|
|
2) |
a) |
|
|
|
b) |
|
|
3) |
|
SABCD = 74 |
|
4) |
a) |
|
|
|
b) |
|
|
5) |
|
p: 2x + 3y – 6 = 0 |
|
6) |
a) |
p: x + 2y + 4 = 0 |
|
|
b) |
|
|
7) |
|
d |
|
8) |
|
d |
|
9) |
|
d |
|
10) |
|
e |
|
11) |
|
a |
|
12) |
|
b |
|
13) |
a) |
všechny nenulové násobky vektoru
|
|
|
b) |
|
|
14) |
|
c |
|
15) |
a) |
a = -1 |
|
|
b) |
b = 2 |
|
16) |
|
8 j |
|
17) |
|
d |
|
18) |
|
|
|
19) |
a) |
|
|
|
b) |
S = 30 j2 |
|
|
c) |
KL: 3x – 5y – 15 = 0 |
|
20) |
|
-
b -
a -
e |
|
21) |
a) |
|
|
|
b) |
q: y – 3 = 0 |
|
22) |
|
-
ne -
ano -
ano -
ano |
|
23) |
|
c |
|
24) |
a) |
|
|
|
b) |
|
|
|
c) |
|
|
25) |
a) |
p: x – 3y + 6 = 0 |
|
|
b) |
18°26´ |
|
|
c) |
18 j2 |
|
26) |
|
|
|
27) |
|
|
|
28) |
|
b |
|
29) |
|
a |
|
30) |
|
e |
