Přípravné příklady ke státní maturitě 9. Kombinatorika, pravděpodobnost a statistika zpět

1) V kódu je na prvním místě jedno z písmen A, B, C nebo D. Na dalších dvou pozicích je libovolné dvojciferné číslo od 11 do 45. (Existují např. kódy B22, A45 apod.)

Určete počet všech takto vytvořených kódů.

2) Určete neznámé číslo k, jestliže platí:

100! = k · 98!

3) Určete neznámé číslo m, jestliže platí:

m! · 2⁸ = 2 · 4 · 6 · 8 · 10 · 12 · 14 · 16

4) Cesta prochází několika křižovatkami. Na každé křižovatce je možné zahnout doleva (L), doprava (P), nebo pokračovat v přímém směru (S). Průjezd dvěma křižovatkami je možné zapsat dvojicí znaků, např. PP.

Kolika možnáými způsoby lze projet dvěma křižovatkami?

a) 9

b) 8

c) 6

d) 5

e) 4

5) Na šachovnici, která má 5 x 5 polí, je vyznačena hlavní a vedlejší diagonála.

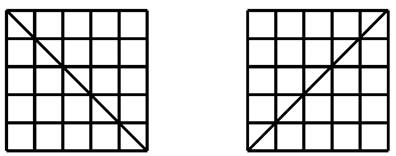
Kolika způsoby je možné na polích šachovnice rozmístit tři stejné figury tak, aby byly všechny tři buď jen na hlavní, nebo jen na vedlejší diagonále?

a) 16

b) 20

c) 30

d) 32

e) 33

6) Frontu na lístky tvoří čtyři dívky a šest chlapců.

Kolika různými způsoby se mohou osoby ve frontě seřadit?

a) 10!

b) 4! + 6!

c) 4 · 6

d) 4! · 6!

e) (4 · 6)!

7) Při zkoušce se zadávají tři otázky. První otázka se vybírá ze skupiny 10 otázek. Další dvě otázky se vybírají z jiné skupiny 20 otázek.

Kolik různých trojic otázek lze při zkoušce zadat?

a) 4 600

b) 4 000

c) 3 800

d) 1 900

e) jiný počet

8) Dětské soutěže se pravidelně účastní malí i velcí chlapci a malá i velká děvčata.

Pravděpodobnost, že zvítězí dívka, je 0,6. Pravděpodobnost, že zvítězí malá dívka, je 0,4.

Malý chlapec zvítězí s pravděpodobností 0,3. Jen občas zvítězí i velký chlapec.

Přiřaďte ke každé otázce správnou odpověď.

- Jaká je pravděpodobnost, že zvítězí chlapec (velký nebo malý)?

- Jaká je pravděpodobnost, že zvítězí velká dívka?

- Jaká je pravděpodobnost, že zvítězí malé dítě (chlapec nebo dívka)?

- Jaká je pravděpodobnost, že nezvítězí malá dívka?

a) 0,2

b) 0,3

c) 0,4

d) 0,5

e) 0,6

f) 0,7

9) V osudí jsou 2 bílé a 3 černé koule. Koule se vytahují po jedné a do osudí se nevracejí.

Přiřaďte ke každému jevu pravděpodobnost, s níž může nastat.

- První tažená koule bude bílá.

- První dvě tažené koule budou černé.

- V první tažené dvojici koulí budou zastoupeny obě barvy.

a)

b)

c)

d)

e)

10) Součet dvaceti položek je 6 000 korun. Po odebrání dvou položek v celkové hodnotě 960 korun se průměrná hodnota položky změní.

Vypočtěte, o kolik korun se změní průměrná hodnota.

11) V obchodním centru zákaznice testovaly tři druhy parfémů A, B, C. Svůj hlas mohly dát pouze jednomu z parfémů. Některé zákaznice se nedokázaly rozhodnout. Preference zákaznic jsou zaznamenány v tabulce.

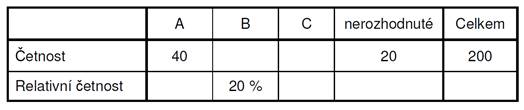
Vypočtěte, kolik zákaznic preferovalo vítězný parfém.

12) Celkem 20 studentů psalo dva závěrečné testy A a B.

V tabulce jsou uvedeny výsledky testů, chybí pouze počet jedniček a dvojek v testu B.

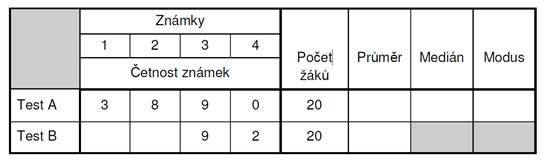
a) Určete medián a modus známek z testu A.

b) V obou testech bylo dosaženo stejné průměrné známky.

Vypočítejte průměrnou známku z testu A a počet jedniček v testu B.

13) Divadlo nabízí pro každé představení celkem 220 vstupenek po 300 korunách a 80 vstupenek po 500 korunách. Během deseti představení bylo šestkrát zcela vyprodáno a čtyřikrát se neprodala právě polovina dražších lístků.

Jaká je průměrná tržba na jedno z deseti přestavení?

a) 98 000 Kč

b) 97 000 Kč

c) 96 000 Kč

d) 95 000 Kč

e) jiná tržba

14) V grafu jsou uvedeny průměrné počty filmových diváků v milionech (sledujte na ose vpravo) a průměrná výše vstupného do kina v době od r. 1988 do r. 2004 (sledujte na ose vlevo). Návštěvnost klesala, ale vstupné se průběžně zvyšovalo.

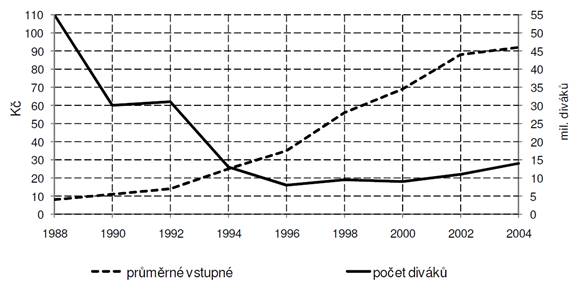
Průměrná roční tržba za vstupné do kina se od roku 1990 do roku 2000:

a) v podstatě nezměnila.

b) zvýšila jen velmi mírně, nejvýše o 20%.

c) zhruba zdvojnásobila.

d) zvýšila téměř pětkrát.

e) zvedla o více než 500%.

15) Na druhý stupeň základní školy v Postrkově chodí místní pěšky, ale všech 56 žáků, kteří jsou z okolních obcí, dojíždí. V diagramu je uvedeno rozložení počtu žáků podle místa bydliště.

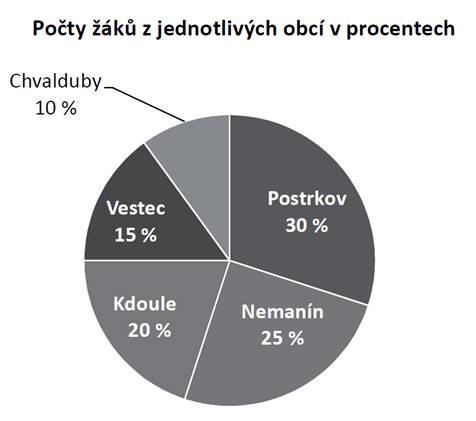
Kolik žáků dojíždí z Nemanína?

a) 14 žáků

b) 18 žáků

c) 20 žáků

d) 24 žáků

e) jiný počet žáků

16) Každý z 20 hráčů prováděl tři trestné hody na koš a třikrát střílel po otočce.

V tabulce jsou hráči rozděleni podle úspěšnosti v obou střeleckých disciplínách. (Například čtyřem hráčům se podařilo proměnit jeden trestný hod a dva hody po otočce.)

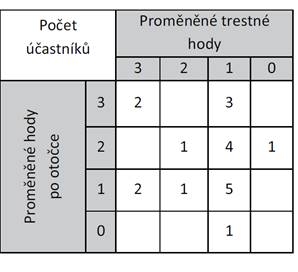
Přiřaďte ke každé otázce odpovídající výsledek:

- Kolik hráčů dalo stejný počet košů v obou disciplínách?

- Kolik hráčů dalo celkem 4 koše?

- Kolik hráčů udělalo alespoň 4 chyby?

- Kolik hráčů bylo lepších při trestných hodech než ve střelbě po otočce?

a) 4

b) 5

c) 6

d) 7

e) 8

f) 9

17) V prvním grafu je uvedeno průměrné časové rozložení všech denních činností paní Nové. Ve druhém grafu je podrobněji popsána náplňjejího volného času.

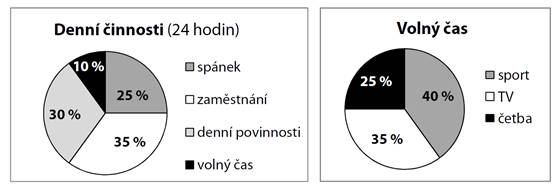
Kolik minut denně věnuje paní Nová četbě?

a) 32 minut

b) 36 minut

c) 38 minut

d) 40 minut

e) 45 minut

18) V osudí jsou 2 bílé a 4 modré koule. Z osudí budou postupně vytaženy 4 koule.

Přiřaďte každému jevu pravděpodobnost, s níž daný jev může nastat.

- V osudí zbydou dvě bílé koule.

- V osudí zbydou dvě modré koule.

- V osudí zbydou dvě koule stejné barvy.

a)

b)

c)

d)

e) jiná hodnota

19) Graf udává četnost známek z písemné práce, avšak počet jedniček není uveden. Medián je 2,5.

Kolik písemných prací bylo oznámkováno?

a) 16

b) 17

c) 18

d) 19

e) jiný počet

20) Ze skupiny 10 dětí se vybírá tříčlenná skupina. Mezi dětmi je jediný Adam a jediná Bohunka. Vybraná skupina musí splňovat ještě některou z dalších stanovených podmínek.

Pro každou z následujících podmínek určete, kolika způsoby je možné tříčlennou skupinu vybrat.

- Ve skupině není Adam ani Bohunka

- Ve skupině je Adam i Bohunka

- Ve skupině je Adam, ale není Bohunka

- Ve skupině je Adam

a) 28

b) 36

c) 56

d) 72

e) 336

f) jiným počtem

21) Graf udává rozložení známek z testu u 20 žáků.

Známku 5 nedostal nikdo.

Rozhodněte o každém z následujících tvrzení, zda je pravdivé, či nikoli.

- Počet žáků, kteří získali známku 1 nebo 2, je stejný jako počet žáků, kteří získali známku 3 nebo 4.

- Aritmetický průměr známek je 2,4.

- Medián je 3.

- Modus je 3.

22) Osm spolužáků (Adam, Bára, Cyril, Dan, Eva, Filip, Gábina a Hana) se má seřadit za sebou tak, aby Eva byla první a Dan předposlední.

Kolik způsoby se mohou spolužáci seřadit?

a) 5 040

b) 2 880

c) 1 440

d) 720

e) jiným počtem

23) Čtyřmístný kód má na prvních třech místech tři různé nenulové číslice a na čtvrtém místě nejmenší z těchto tří číslic (např. 5282, 7565, 5211 apod.).

Kolik různých kódů vyhovuje popisu?

a) méně než 504

b) 504

c) 512

d) 720

e) více než 720

24) Hází se současně dvěma hracími kostkami – červenou a zelenou.

Jaká je pravděpodobnost, že na červené kostce padne číslo větší než 2?

a) menší než

b)

c)

d)

e) větší než

25) Družstvo základní školy se zúčastní televizní soutěže. Jméno družstva vybírali žáci ZŠ ze tří návrhů, a to „Machři“, „Puštíci“ a „Vikingové“. Výsledky hlasování znázorňují kruhové diagramy.

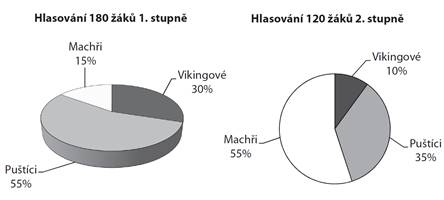
Kolik procent hlasujících žáků vybralo jméno „Vikingové“?

a) 20 %

b) 22 %

c) 33 %

d) 40 %

e) jiný počet procent

26) Je dána rovnice s neznámou :

Jaké je řešení rovnice?

a) 11

b) 10

c) 9

d) 8

e) jiné řešení

27) Ze 3 chlapců a 4 dívek se losují dva hráči do hry. První vylosovaný bude kapitán, druhý kormidelník.

Jaká je pravděpodobnost, že kapitánem bude chlapec?

a)

b)

c)

d)

e) jiná pravděpodobnost

28) Ze čtvrtletní práce získalo 22 žáků následující známky:

3, 4, 2, 5, 4, 3, 4, 2, 1, 4, 3, 4, 5, 2, 4, 3, 2, 4, 5, 1, 3, 4

a) Určete medián známek ze čtvrtletní práce ve 3.B

b) Určete modus známek ze čtvrtletní práce ve 3.B

29) Trojciferné číslo má splňovat následující podmínky: V dekadickém zápise je na místě stovek sudá číslice, na místě desítek lichá číslice a na místě jednotek libovolná číslice, která nebyla požita na předchozích místech. (Vyhovují např. čísla 492, 430, 813.)

Určete počet všech čísel, která splňují dané podmínky.

30) Ve skupině jede 50 cyklistů. celkem 10 z nich se provinilo konzumací alkoholických nápojů před jízdou.

Policejní hlídka vybere ze skupiny náhodně 5 cyklistů.

Jaké je pravděpodobnost, že mezi vybranými cyklisty nebude žádný z 10 provinilců?

Hodnota pravděpodobnosti je zaokrouhlena na setiny.

a) 0,31

b) 0,40

c) 0,49

d) 0,58

e) jiná pravděpodobnost

31) Čtyřciferné přirozené číslo se má sestavit ze čtyř různých číslic. Na prvním místě má být číslice 2 a na místě desítek lichá číslice.

(Daným podmínkám vyhovují například čísla 2 430 a 2 793.)

Kolik různých čísel je možné uvedeným způsobem sestavit?

a) 21

b) 240

c) 280

d) 360

e) jiný počet

32) Z 25 žáků jedné třídy domácí úkol 3 žáci nevypracovali, 6 žáků jej vypracovalo chybně a zbývající žáci jej vypracovali správně.

Učitel náhodně vybere dvojici žáků.

Jaká je pravděpodobnost, že oba vybraní žáci budou mít úkol vypracován správně?

a)

b)

c)

d)

e) jiná pravděpodobnost

33) A = 1 000! · 3!

B = 999! · 5!

Kolikrát je číslo A větší než číslo B?

a) méně než 10krát

b) 10krát

c) 20krát

d) 50krát

e) více než 50krát

34) Z množiny po sobě jdoucích přirozených čísel od 1 do 100 se náhodně vybere jedno číslo.

Vypočtěte pravděpodobnost, že:

a) vybrané číslo je dělitelné osmi

b) vybrané číslo je dělitelné dvěma, ale není dělitelné osmi

35) Každý člen výpravy (řidič, dvě učitelky a 27 studentů) si zakoupil jednu slosovatelnou vstupenku. Z těchto 30 vstupenek budou čtyři vylosovány a jejich majitelé získají některou z cen.

Jaká je pravděpodobnost, že všechny čtyři ceny získají jen studenti?

Hodnota pravděpodobnosti je zaokrouhlena na setiny.

a) 0,12

b) 0,15

c) 0,64

d) 0,68

e) jiná pravděpodobnost

36) Soutěž má dvě kola. Body z obou kol se sčítají.

Soutěžící byli na počátku soutěže rozděleni do dvou skupin.

V těchto skupinách absolvovali první i druhé kolo soutěže.

Průměrné výsledky jsou uvedeny v tabulce.

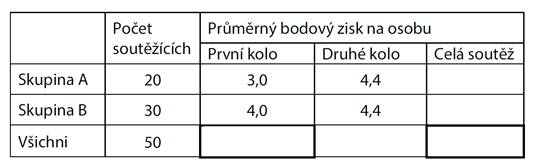
a) Vypočtěte průměrný bodový zisk na osobu v prvním kole soutěže.

(Počítejte se všemi 50 soutěžícími.)

b) Vypočtěte průměrný bodový zisk na osobu v celé soutěži.

(Počítejte se všemi 50 soutěžícími.)

1) Tajný kód splňuje následující 3 pravidla:

- kód může obsahovat pouze číslice 1, 2, 3, 4, 5, 6

- žádné číslice se v kódu neopakují

- počet číslic v kódu udává první číslice kódu

(Uvedeným pravidlům vyhovují kódy 21, 326, 4325 a další.)

a) Uveďte počet všech kódů, které mají na prvním místě číslici 3.

b) Uveďte počet všech kódů, které mají na prvním místě číslici 4, 5 nebo 6.

1) Každá z 9 různých karet obsahuje jeden ze tří obrazců (trojúhelník, čtverec, kruh) v jedné ze tří barev (šedá, černá,modrá).

Karty zamícháme a náhodně odebereme 2 karty.

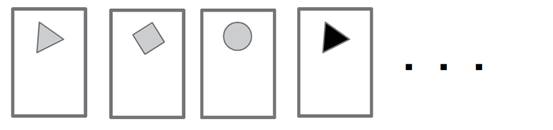
Jaká je pravděpodobnost, že žádná z obou odebraných karet nebude obsahovat ani trojúhelník, ani obrazec černé barvy?

a)

b)

c)

d)

e) jiná pravděpodobnost

zpět

Výsledky:

1)		4 · 35 = 140
2)		k = 9 900
3)		m = 8
4)		a
5)		b
6)		a
7)		d
8)		c, a, f, e
9)		b, e, d
10)		klesne o 20 korun
11)		100
12)	a)	medián 2; modus 3
	b)	průměrná známka 2,3; počet jedniček 7
13)		a
14)		c
15)		c
16)		- e - c - d - a
17)		b
18)		- a - e - c
19)		a
20)		- c - f - a - b
21)		- ano - ano - ne - ano
22)		d
23)		b
24)		d
25)		b
26)		a
27)		b
28)	a)	medián 3,5
	b)	modus 4
29)		160 čísel
30)		a
31)		c
32)		a
33)		d
34)	a)	0,12
	b)	0,38
35)		c
36)	a)	3,6
	b)	8,0
37)	a)	20
	b)	300
38)		a