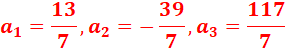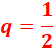zpět na zadání – geometrická posloupnost
Součet tří po sobě jdoucích členů geometrické posloupnosti je 13. Podíl
třetího a prvního člena je 9. Urči členy této posloupnosti.
![]()
![]()
a2 a a3 vyjádříme
pomocí a1 a q:
![]()
![]()
Po dosazení do původních rovnic
dostaneme:
![]()
![]()
Z druhé z těchto rovnic vyjádříme
q:
![]()
![]() nebo
nebo ![]()
tato q dosadíme do první rovnice
|
pro q = 3 dostaneme:
z čehož dostaneme:
|
pro q = -3 dostaneme:
z čehož dostaneme:
|
|
řešení 1 (q = 3):
|
řešení 2 (q = -3):
|
![]()
![]()
![]() nebo
nebo ![]()
|
pro q = 2:
|
pro q = -2:
|
řešení 1 ![]() :
:
![]()
řešení 2 ![]() :
:
![]()
První rovnici vynásobíme -1 a rovnice
potom sečteme, tím dostaneme a2.
![]()
![]()
![]()
První rovnici vyjádříme pomocí a2: ![]()
![]()
![]()
![]()
![]()
![]()
Z toho vyplývá: ![]()
![]()
Z toho vyplývá: ![]()